画像をダウンロード 一次関数 変化の割合 問題 917342-一次関数 変化の割合 問題

中2数学 一次関数の値の変化 変化の割合 の定期テスト過去問分析問題 ダイスト
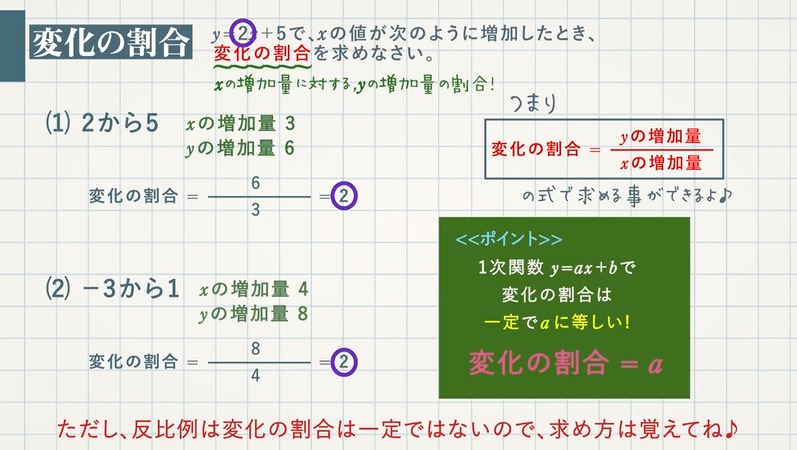
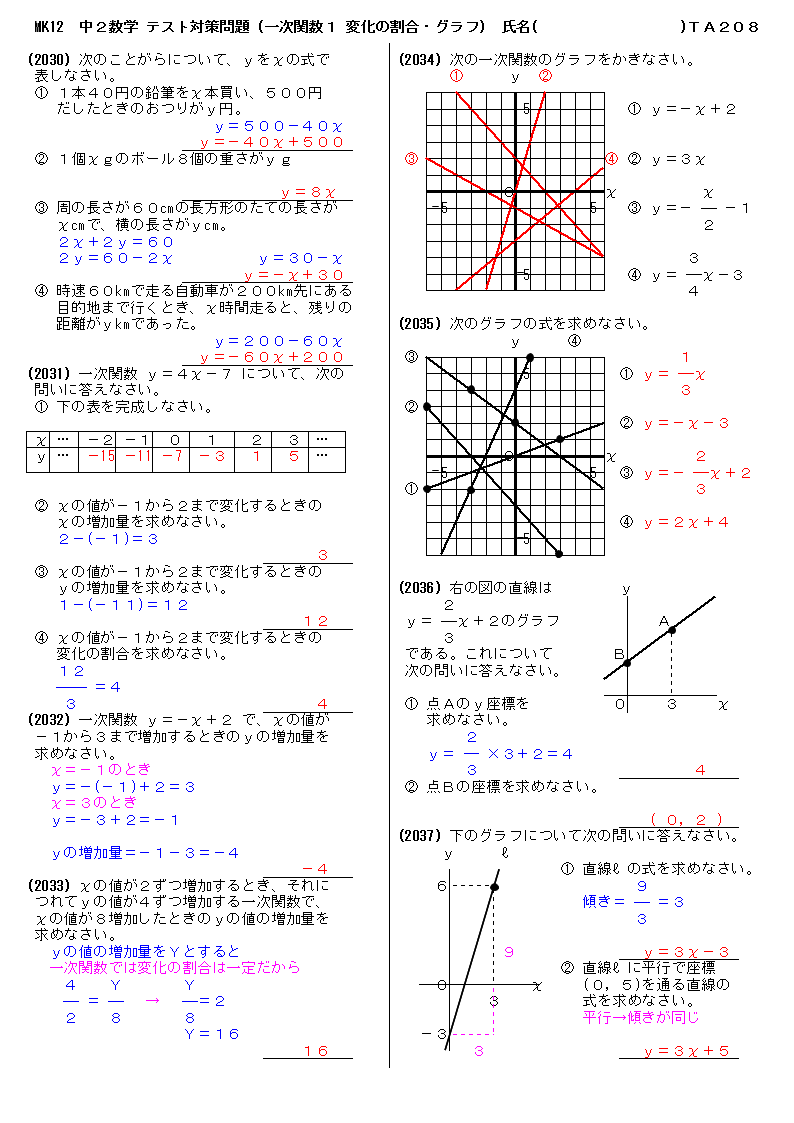
一次関数 = y = a x b では 変化の割合は 「 a 」と等しく 「一定」です (1)では x が0から4に増加した時 x が1から3に増加した時 の「変化の割合」を計算しています どちらも中学数学で学習する一次関数の基本問題を全パターン解説します。 にゃんこ これらの練習問題は、中学2年生の数学の定期テスト対策にご利用ください。 一次関数の式や座標を求める練習問題:基本レベル 傾きがわかる 点(2,1)を通り、 傾き が-4の
一次関数 変化の割合 問題
一次関数 変化の割合 問題-第2学年 3 一次関数 知識・技能の習得を図る問題 年 組 号 氏名 練習問題① 次の(1),(2)の各問いに答えなさい。 (1) 下のアからオの中に,y が x の一次関数であるものがあります。 正しいものをすべて選今回は中2で学習する 『一次関数』の単元から 直線の式の求め方について解説していくよ! ここでは、いろんなパターンの問題が出題されるので パターン別に例題を使って解説していきます。 傾き、切片が与えられる (1)傾きが5で、切片が-2である
中学数学の一次関数の練習問題 基本全パターンを解説 坂田先生のブログ
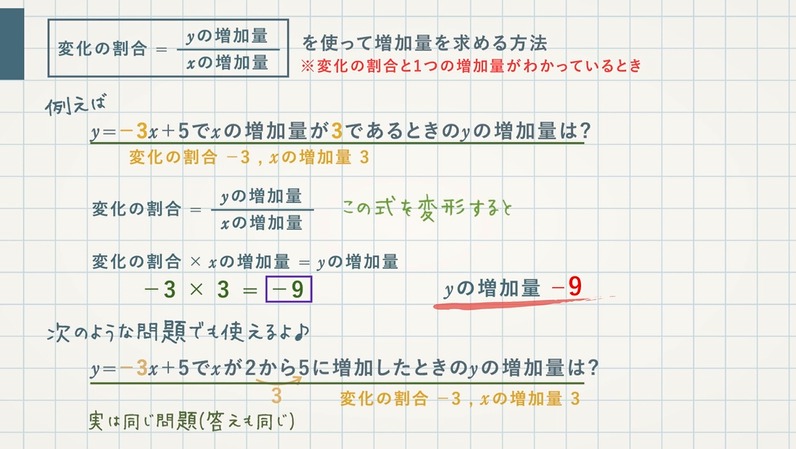
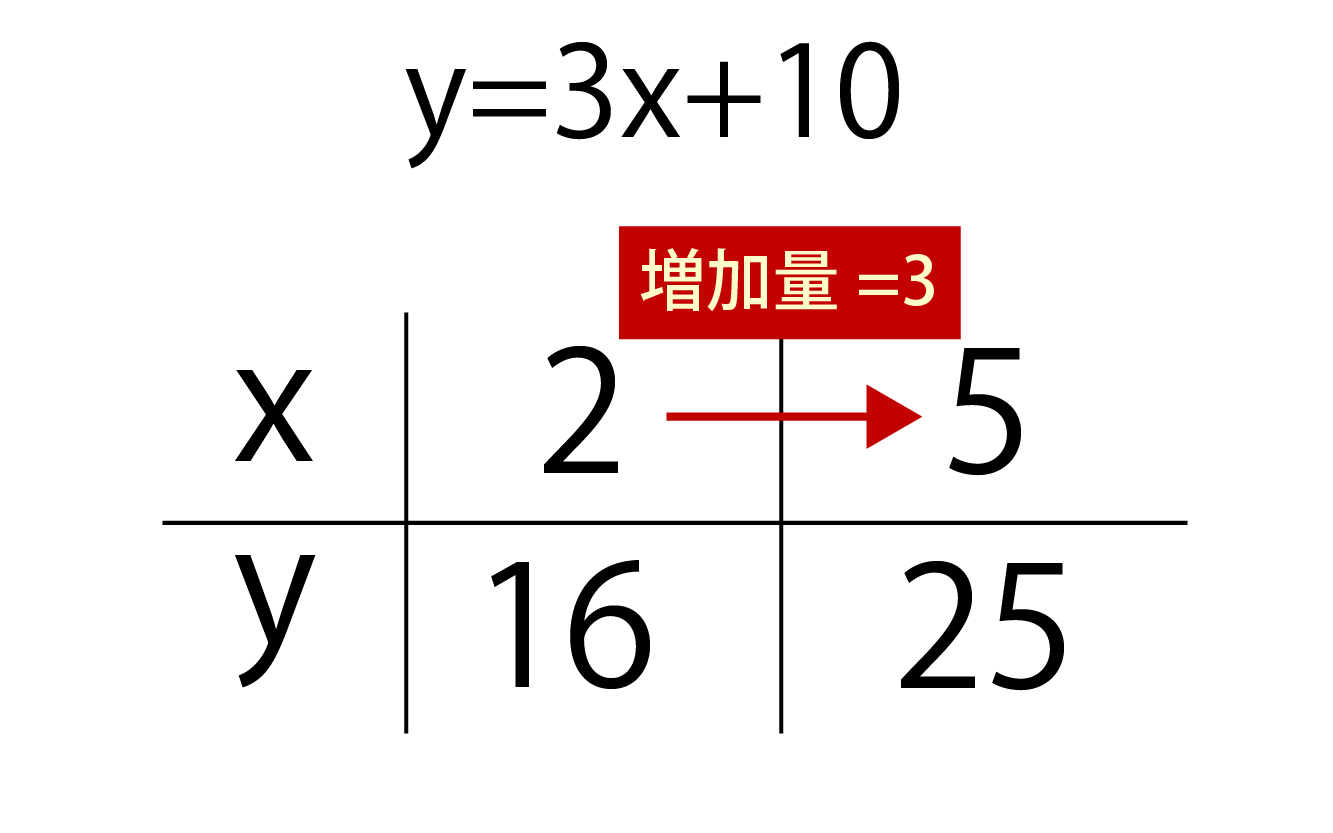
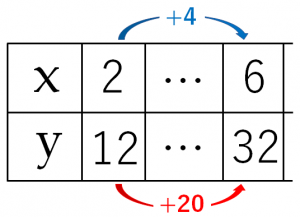
練習問題4 以下の一次関数のグラフをかきなさい。 ただし、 x の変域は( )の中のときとする。 1 y =3 x x 2 y = 1 2 x x 3 y =- x x 4 y =- 2 3 x x <前:L19 一次関数の値とその変化の割合 の問題 L 一次関数のグラフ の解答:次>簡単な問題ですが、テストがちかいので、できれば詳しく、早めに教えて下さいy=2x3でxが1から3まで増加するときの変化の割合は?よろしくお願いします 数学 締切済 教え変化の割合 一次関数の変化の割合に関する問題です。 一次関数では傾き(y=axb のa )が変化の割合になります。 最初はxの増加量、yの増加量の計算方法をしっかり身につけましょう。 *現在作成中です。問題は追加する予定です。 変
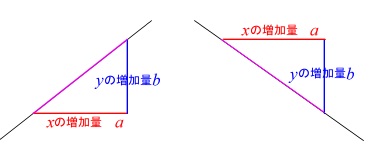
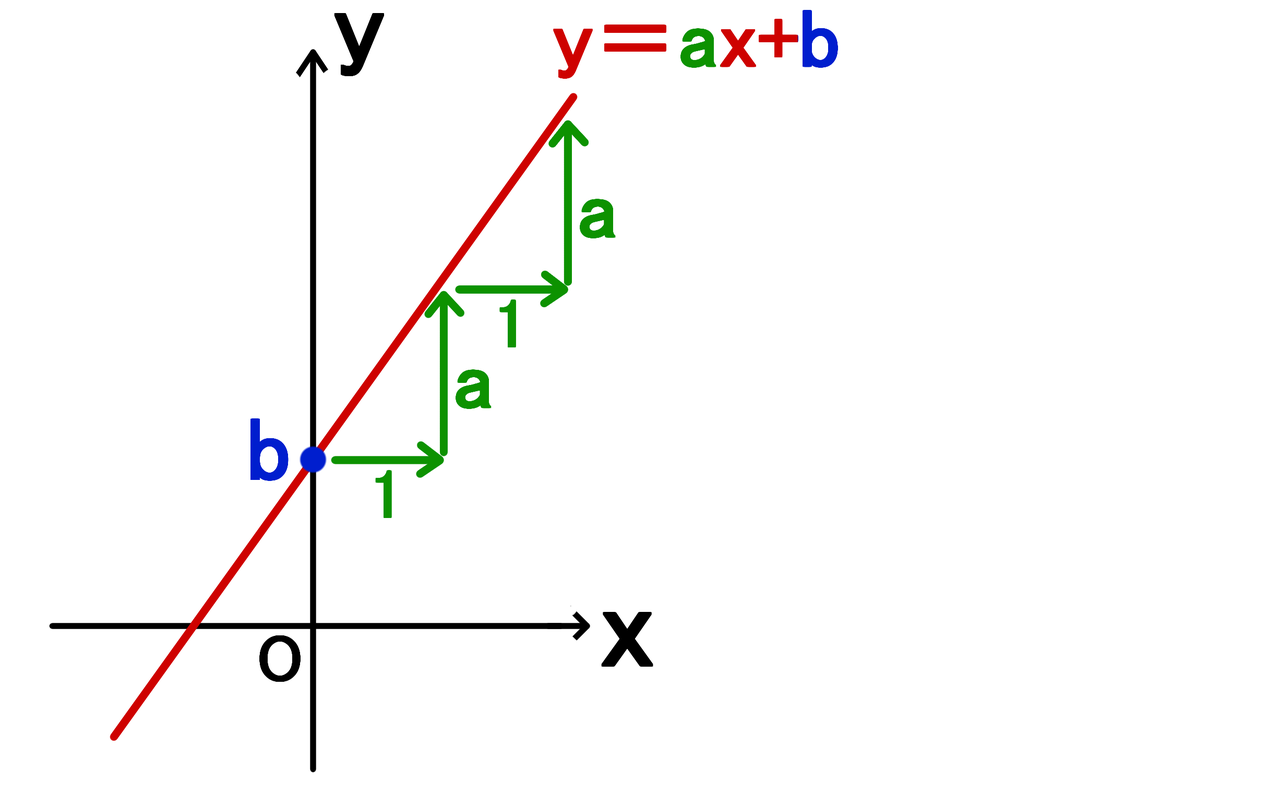
問9 変化の割合が一次関数y=3x-4の変化の割合に等しく,x=-1のときy=2となる一次関数の式を求めなさい。 (北海道 03年度) 問10 2つの方程式 -2x+y=3と2ax+3y=5のグラフが,平行となるようなaの値を求めなさい。 (茨城県 03年度) a=変化の割合と一次関数の関係 変化の割合は、一次関数の傾きaと同じ値です。一次関数とは、下記に示す関数です。 aは傾き、bは切片(せっぺん)といいます。下図に一次関数のグラフを示します。 上図の通り一次関数の傾きaは、yの増加量÷xの増加量で1次関数の基礎 式の求め方 座標の求め方 変化の割合 一次関数(総合問題) 一次関数 (ダイヤグラム) 一次関数 (動点) 一次関数 (ダイヤグラム2) 一次関数 (面積二等分) 一次関数 (三角形の面積)
一次関数 変化の割合 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
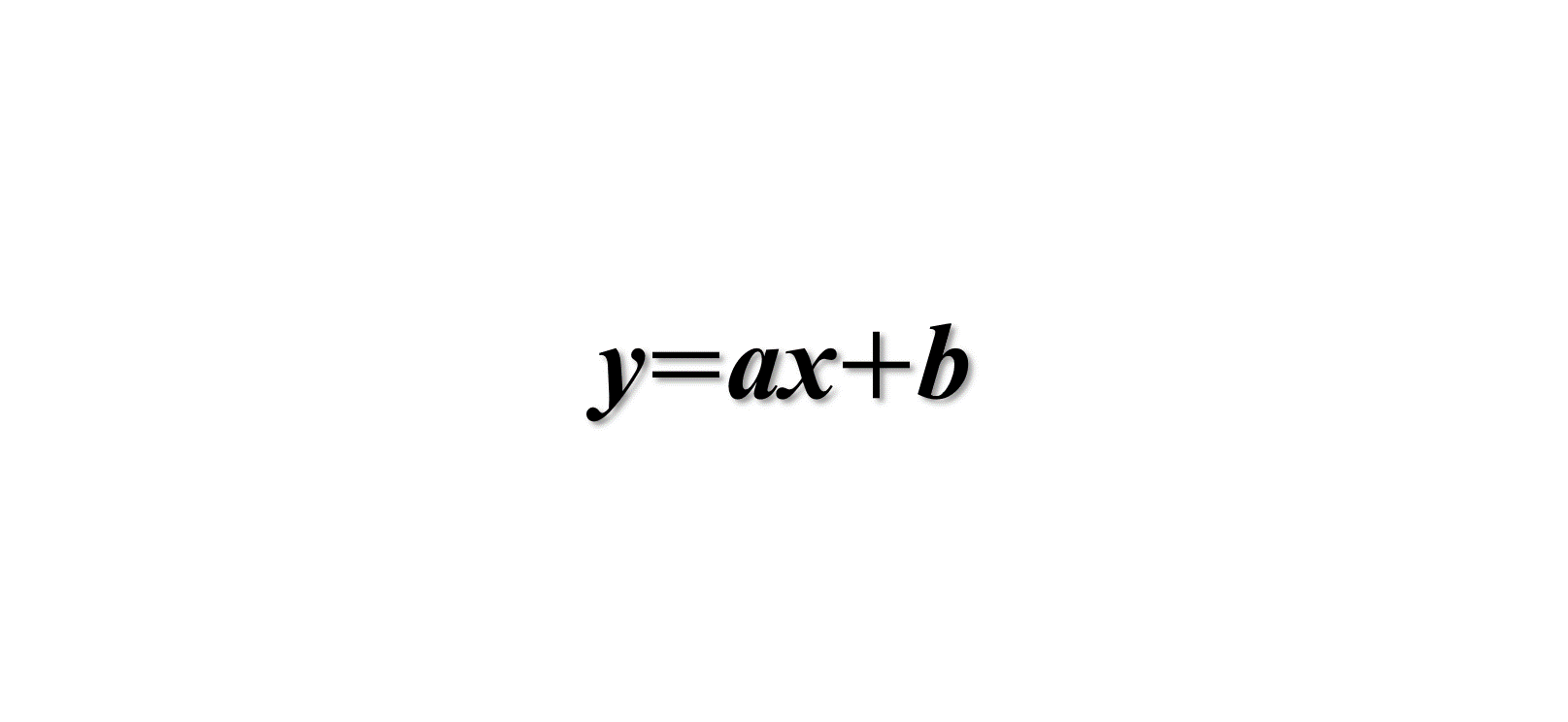 |  |  |
 |  | |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「一次関数 変化の割合 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
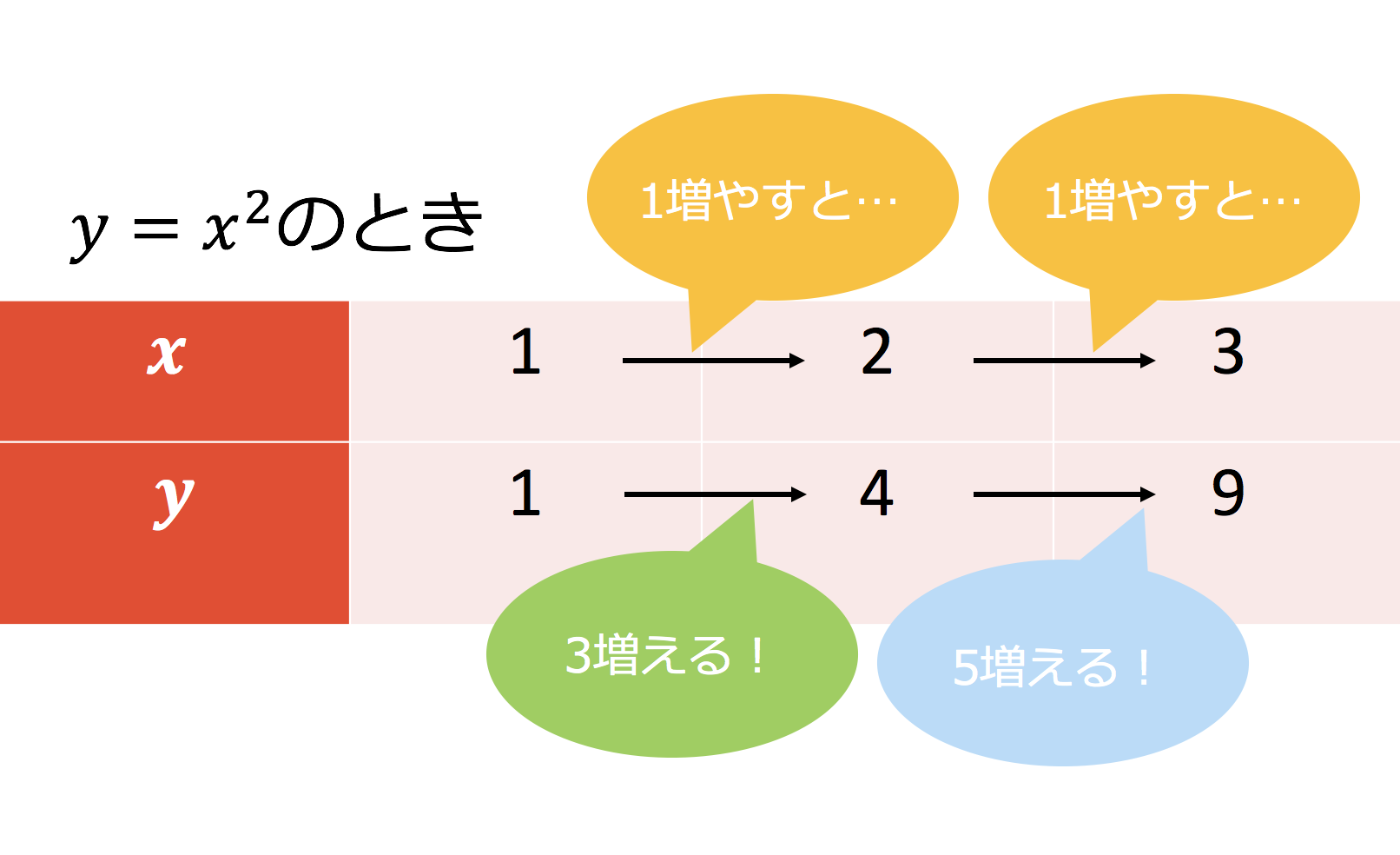
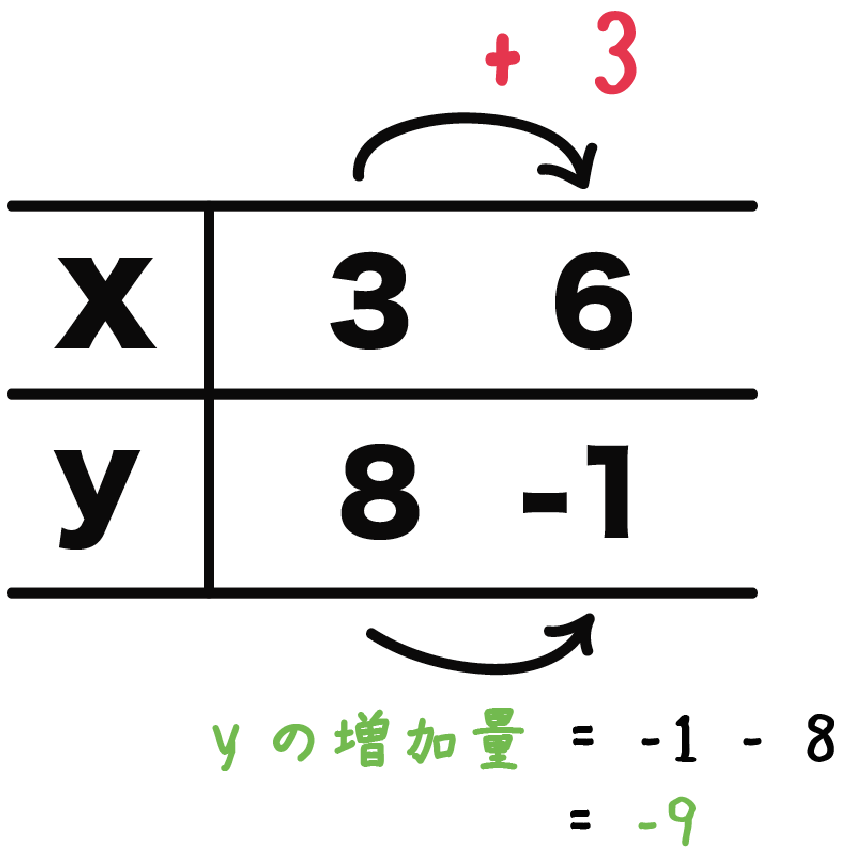
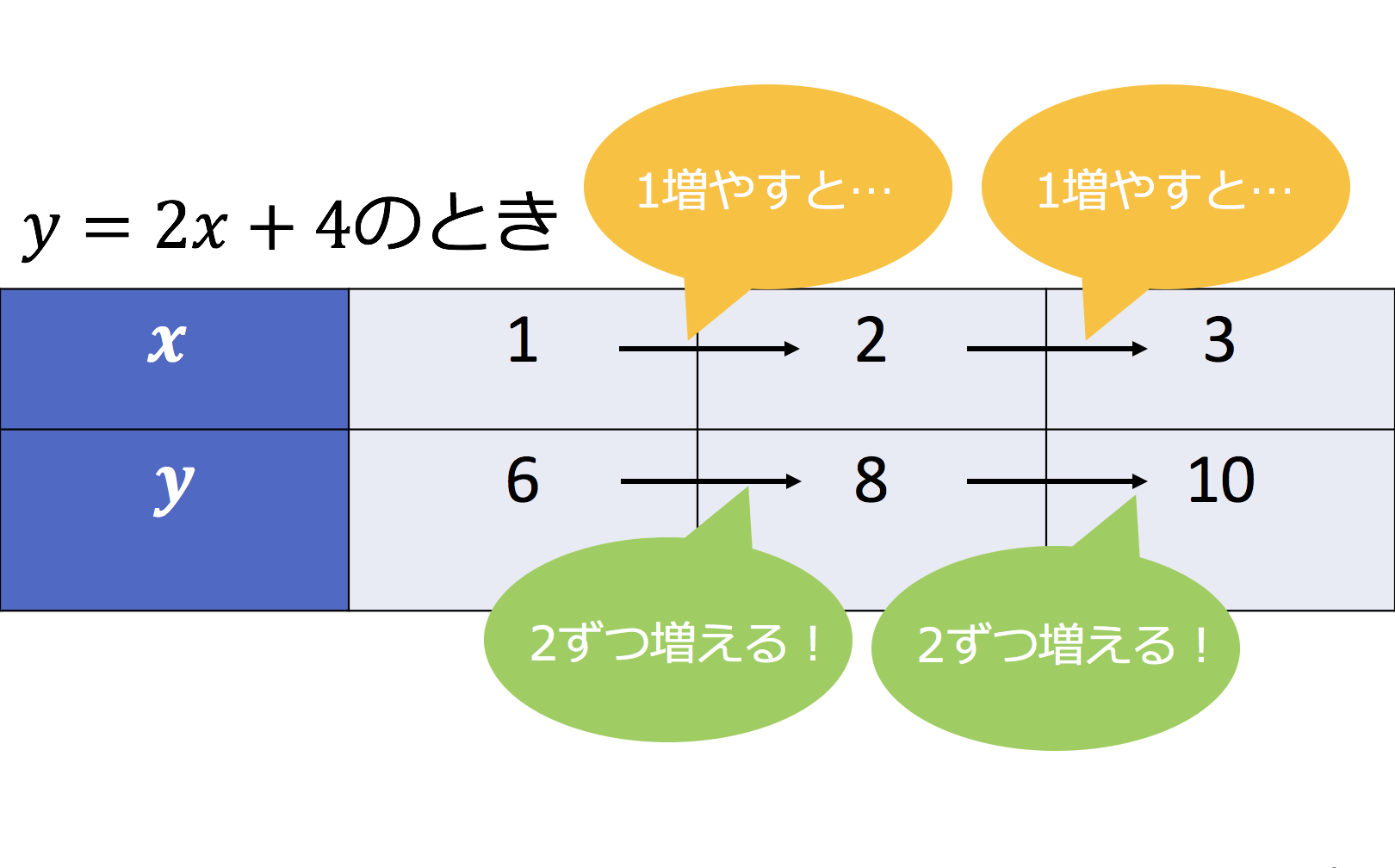
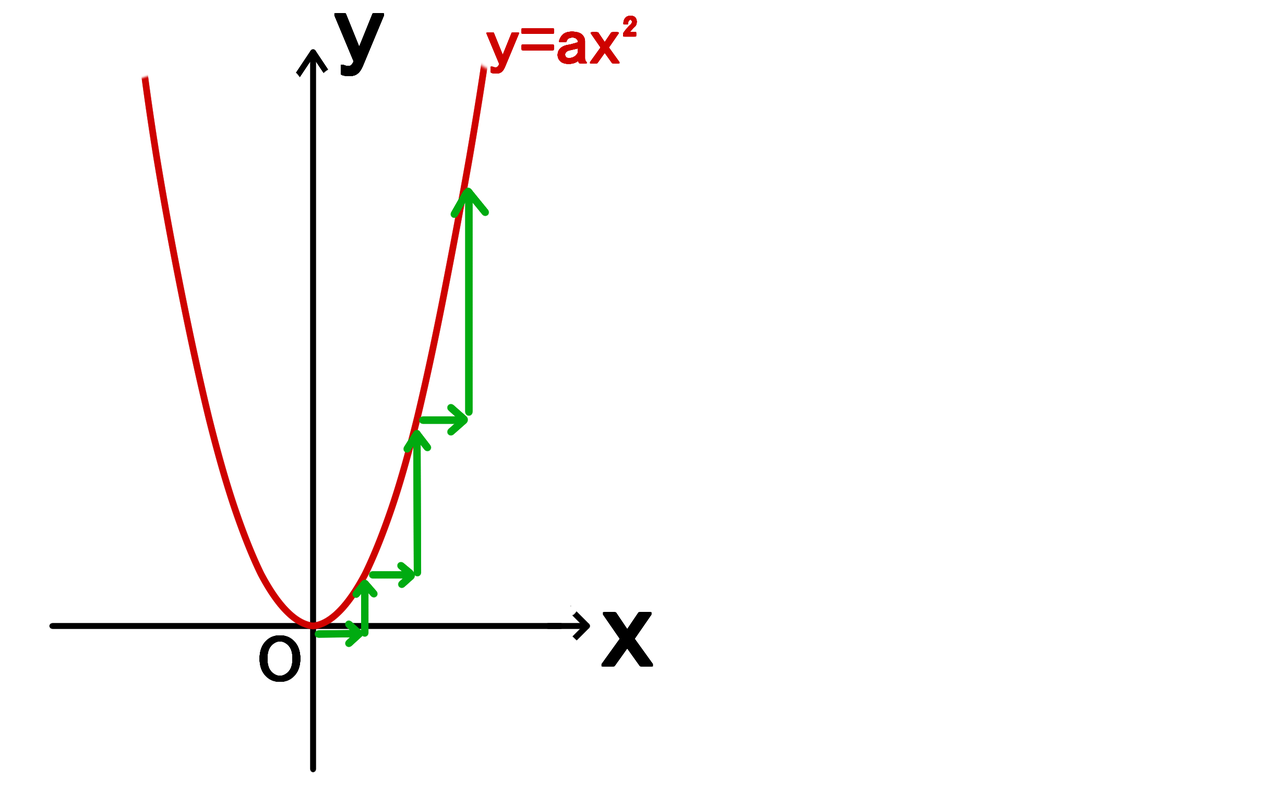
変化の割合は増え方が一定であることを意味します。 グラフで言う傾きと一致します。 増加量は目に見えないので苦手意識をもつ人も多いようですが、表を頭の中で描ければそんなに難しくはありません。 問題を解くことで慣れていきましょう。変化の割合の求め方とは? 変化の割合の求め方は こうでしたね! この求め方は 比例だろうが反比例だろうが一次関数や二次関数においても どんな関数でも求め方は同じです。 一次関数の場合は、傾きと同じ値になる。 2乗に比例する関数の場合は
Incoming Term: 一次関数 変化の割合 問題,
コメント
コメントを投稿